131 Percent Of 93
micasatop
Sep 25, 2025 · 5 min read
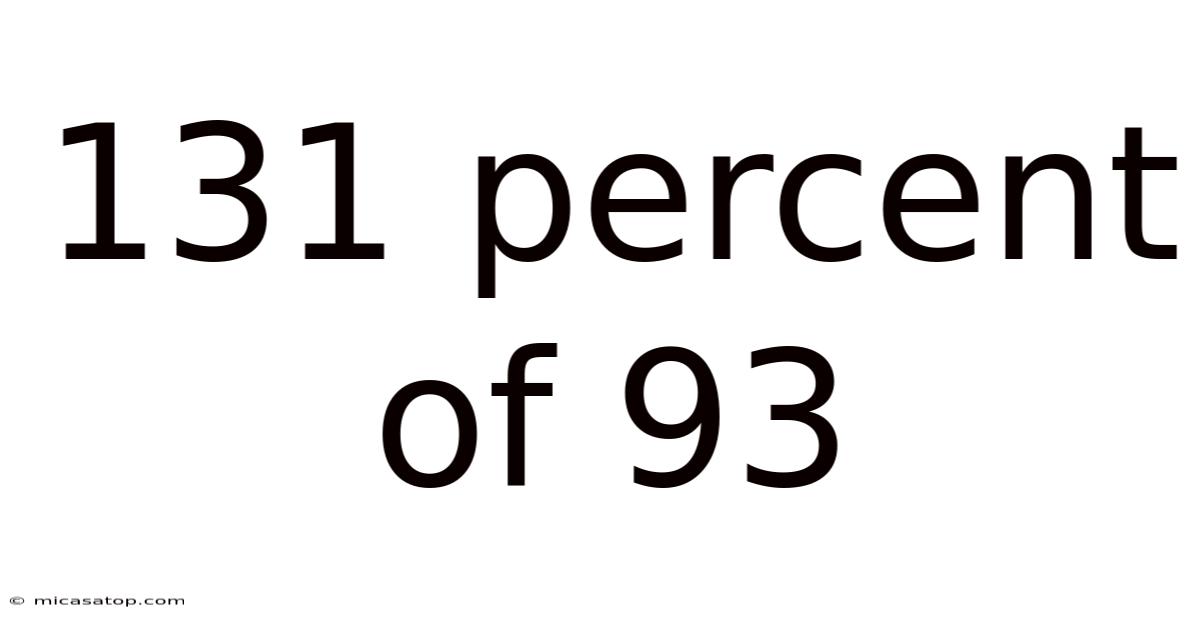
Table of Contents
Decoding 131 Percent of 93: A Deep Dive into Percentages and Their Applications
Finding 131 percent of 93 might seem like a simple mathematical problem, but it opens the door to understanding a fundamental concept with vast applications across various fields. This article will not only show you how to calculate 131% of 93 but also delve into the broader meaning of percentages, their practical uses, and some common misconceptions. We'll explore different calculation methods, discuss the significance of exceeding 100%, and illustrate its relevance in real-world scenarios. Let's embark on this journey of numerical exploration!
Understanding Percentages: The Foundation
Before tackling the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" signifies "per hundred" or "out of 100." For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Percentages are invaluable tools because they provide a standardized way to compare proportions and ratios. Whether you're analyzing financial data, evaluating test scores, or understanding sales growth, percentages offer a clear and concise representation of relative values.
Calculating 131 Percent of 93: Methods and Explanation
There are several ways to calculate 131% of 93. Let's explore the most common methods:
Method 1: Using Decimal Conversion
This is perhaps the most straightforward approach. We first convert the percentage to a decimal by dividing it by 100. 131% becomes 131/100 = 1.31. Then, we multiply this decimal by the number we're interested in (93):
1.31 * 93 = 121.83
Therefore, 131% of 93 is 121.83.
Method 2: Breaking Down the Calculation
We can also break down the calculation into two parts:
- 100% of 93: This is simply 93.
- 31% of 93: To find this, we convert 31% to a decimal (0.31) and multiply by 93: 0.31 * 93 = 28.83
Finally, we add the two parts together: 93 + 28.83 = 121.83
This method offers a clearer understanding of the components contributing to the final result.
Method 3: Using Proportions
We can set up a proportion to solve this problem:
Let x be 131% of 93
x / 93 = 131 / 100
Cross-multiplying gives:
100x = 93 * 131
100x = 12183
x = 12183 / 100
x = 121.83
This method highlights the fundamental relationship between percentages and proportions, emphasizing the equivalence between the ratios.
The Significance of Percentages Exceeding 100%
It's important to note that percentages can, and often do, exceed 100%. This doesn't signify an error; instead, it indicates that the value being expressed is greater than the original value. In the case of 131% of 93, it means the result (121.83) is 131% of the original number 93. This situation frequently arises in various contexts, including:
- Growth and Increase: Imagine a business experiencing a 131% increase in sales. This means the sales have grown to 131% of their previous level.
- Financial Investments: An investment might yield a return exceeding 100%, signifying significant gains.
- Data Analysis: A dataset might show a percentage greater than 100% if comparisons involve multiple categories or additive factors.
- Error Calculations: In scientific experiments or engineering calculations, errors or deviations might exceed the nominal value, resulting in percentage values over 100%.
Real-World Applications: Where Percentages Matter
The concept of percentages extends far beyond simple mathematical exercises. Its practical applications permeate diverse fields:
- Finance: Calculating interest rates, taxes, discounts, profits, and losses all rely heavily on percentage calculations. Understanding percentage changes in stock prices or investment returns is crucial for financial planning.
- Business: Analyzing sales figures, market share, profit margins, and growth rates all involve the use of percentages. Businesses use percentages to track key performance indicators (KPIs) and make informed decisions.
- Science: Percentages are used to express concentrations (e.g., percentage of a certain chemical in a solution), error margins, and statistical probabilities. Scientific research relies heavily on data analysis involving percentages.
- Education: Test scores, grade point averages (GPAs), and other academic metrics are often expressed as percentages, providing a standardized way to compare student performance.
- Everyday Life: Calculating tips in restaurants, understanding discounts at stores, or even figuring out the percentage of ingredients in a recipe all involve percentage calculations.
Common Misconceptions about Percentages
Several common misconceptions surrounding percentages can lead to errors in calculations and interpretations:
- Adding Percentages Directly: You cannot simply add percentages directly unless they refer to the same base value. For example, a 10% increase followed by a 20% increase is not equivalent to a 30% increase.
- Confusing Percentage Change with Absolute Change: The percentage change and the absolute change are distinct. A large percentage change might represent a small absolute change, and vice-versa, depending on the initial value.
- Misinterpreting Percentage Points: Percentage points refer to the arithmetic difference between two percentages, not a percentage change. For example, an increase from 10% to 20% is a 10 percentage point increase, but a 100% percentage change.
Frequently Asked Questions (FAQ)
-
What if I need to calculate a percentage less than 100%? The process remains the same. Convert the percentage to a decimal and multiply by the original number. For example, to find 75% of 93, you would calculate 0.75 * 93 = 69.75.
-
How do I calculate the percentage increase or decrease between two numbers? Find the difference between the two numbers, divide this difference by the original number, and multiply by 100. For example, to find the percentage increase from 50 to 75, you would calculate [(75-50)/50] * 100 = 50%.
-
Can I use a calculator to calculate percentages? Yes, most calculators have a percentage function (%) that simplifies the calculation.
-
Are there online tools for percentage calculations? Yes, numerous online calculators and converters are readily available to assist with percentage calculations.
Conclusion: Mastering the Power of Percentages
Understanding percentages is a fundamental skill with widespread applicability. This article has demonstrated how to calculate 131% of 93 using various methods, highlighted the significance of percentages exceeding 100%, and explored real-world applications across diverse fields. By grasping the principles discussed here and overcoming common misconceptions, you'll be equipped to confidently tackle percentage-related problems and interpret percentage-based data in your daily life, professional endeavors, and academic pursuits. Remember, the seemingly simple calculation of 131% of 93 unveils a much broader understanding of a critical mathematical and analytical tool.
Latest Posts
Related Post
Thank you for visiting our website which covers about 131 Percent Of 93 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.